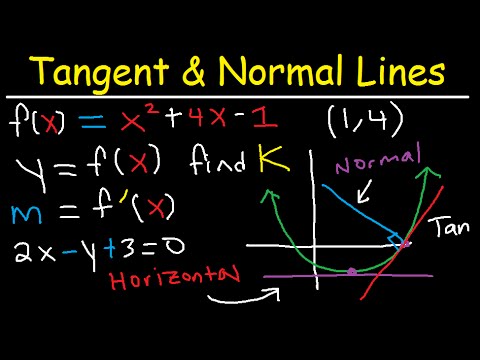
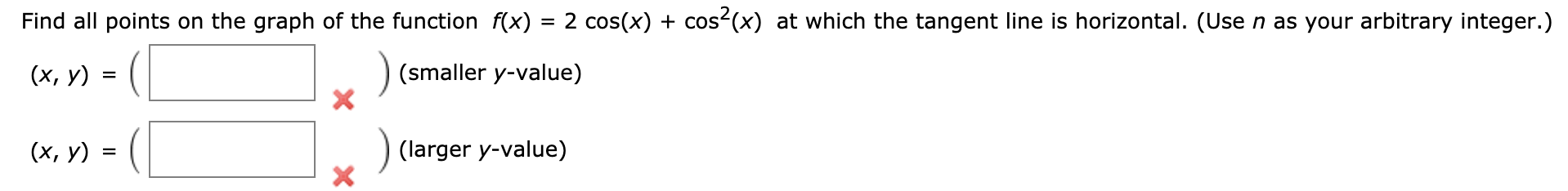A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Therefore, when the derivative is zero, the tangent line is horizontal. To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function. We'll also look at where to find vertical tangent lines, and where to find horizontal tangent lines, since that's something you'll be asked to do often.
Horizontal tangent lines exist where the derivative of the function is equal to 0, and vertical tangent lines exist where the derivative of the function is undefined. The slope of the tangent line to a curve measures the instantaneous rate of change of a curve. We can calculate it by finding the limit of the difference quotient or the difference quotient with increment \(h\). Just as we have used two different expressions to define the slope of a secant line, we use two different forms to define the slope of the tangent line. As before, the choice of definition will depend on the setting.
Now that we have formally defined a tangent line to a function at a point, we can use this definition to find equations of tangent lines. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century.
Many calculus books will treat this as its own problem. We however, like to think of this as a special case of the rate of change problem. In the velocity problem we are given a position function of an object, \(f\left( t \right)\), that gives the position of an object at time \(t\). Then to compute the instantaneous velocity of the object we just need to recall that the velocity is nothing more than the rate at which the position is changing.
The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point.
Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. Together we will walk through three examples and learn how to use the point-slope form to write the equation of tangent lines and normal lines. As we have seen throughout this section, the slope of a tangent line to a function and instantaneous velocity are related concepts. Each is calculated by computing a derivative and each measures the instantaneous rate of change of a function, or the rate of change of a function at any point along the function.
Note that where functions have vertical tangent lines, they are not differentiable at that point. The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.
Since the slope is not defined, there is no vertical tangent lines to the given curve. Intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point. However, in three-dimensional space, many lines can be tangent to a given point. If these lines lie in the same plane, they determine the tangent plane at that point.
A tangent plane at a regular point contains all of the lines tangent to that point. A more intuitive way to think of a tangent plane is to assume the surface is smooth at that point . Then, a tangent line to the surface at that point in any direction does not have any abrupt changes in slope because the direction changes smoothly. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope.
Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. Differentiate the equation of the circle and plug in the values of x,y in the derivative. Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point. Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation.
Secant lines approximating the tangent line.So far we have found the slopes of two secant lines that should be close to the slope of the tangent line, but what is the slope of the tangent line exactly? Since the tangent line touches the circle at just one point, we will never be able to calculate its slope directly, using two "known" points on the line. What we need is a way to capture what happens to the slopes of the secant lines as they get "closer and closer" to the tangent line. As \(\Delta x\) is made smaller , \(7+\Delta x\) gets closer to 7 and the secant line joining \((7,f)\) to \((7+\Delta x,f(7+\Delta x))\) shifts slightly, as shown in Figure 4.1.
This is actually quite difficult to see when \(\Delta x\) is small, because of the scale of the graph. The values of \(\Delta x\) used for the figure are \(1\text\) \(5\text\) \(10\) and \(15\text\) not really very small values. The tangent line is the one that is uppermost at the right hand endpoint. The tangent at A is the limit when point B approximates or tends to A.
As with the tangent line problem all that we're going to be able to do at this point is to estimate the rate of change. So, let's continue with the examples above and think of \(f\left( x \right)\) as something that is changing in time and \(x\) being the time measurement. Again, \(x\) doesn't have to represent time but it will make the explanation a little easier. While we can't compute the instantaneous rate of change at this point we can find the average rate of change. Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph.
In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency. Observe the graph of the curve notice that, the curve has horizontal tangent lines at the points and . Likewise, we can even extend this concept to writing equations of normal lines, which are also called perpendicular lines.
The only difference will be that we will simply use the negative reciprocal slope of the line tangent. Therefore, let's formally lay out the steps for writing the tangent line equation to a curve, as this particular skill is pivotal for future lessons dealing with linearization and differentials. Use a straight edge to verify that the tangent line points straight up and down at that point. If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point. We could estimate the slope of L from the graph, but we won't. Instead, we will use the idea that secant lines over tiny intervals approximate the tangent line.
Also, do not worry about how I got the exact or approximate slopes. We'll be computing the approximate slopes shortly and we'll be able to compute the exact slope in a few sections. The vertical tangent to a curve occurs at a point where the slope is undefined . This can also be explained in terms of calculus when the derivative at a point is undefined. There is no vertical tangent lines to the given curve. Answer We have been given a position function, but what we want to compute is a velocity at a specific point in time, i.e., we want an instantaneous velocity.
Vertical tangent lines occur at the points (-4, -1) and (2, -1). No, the curve cannot have a horizontal tangent where it crosses the x-axis. 2) Plug x value of the indicated point into f ' to find the slope at x.
3) Plug x value into f to find the y coordinate of the tangent point. 4) Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line. ¶Before we embark on setting the groundwork for the derivative of a function, let's review some terminology and concepts. Remember that the slope of a line is defined as the quotient of the difference in y-values and the difference in x-values. In reality there probably won't be 15 cm3 more air in the balloon after an hour.
The rate at which the volume is changing is generally not constant so we can't make any real determination as to what the volume will be in another hour. In calculus, differential approximation is a way to approximate the value of a function close to a known value. It is just another name for tangent line approximation. In other words, you could say "use the tangent line to approximate a function" or you could say "use differentials to approximate a function"; They mean the same thing. Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis.
The method works well when you can't use other methods to find zeros of functions, usually because you just don't have all the information you need to use easier methods. While Newton's method might look complex, all you're actually doing is finding a tangent line, then another tangent line, and repeat, until you think you're close enough to the actual solution. A tangent line is a line that touches a graph at only one point and is practically parallel to the graph at that point.
It is the same as the instantaneous rate of change or the derivative . The instantaneous rate of change is the slope of the tangent line at a point. A derivative function is a function of the slopes of the original function. You can find the instantaneous rate of change of a function at a point by finding the derivative of that function and plugging in the x -value of the point.
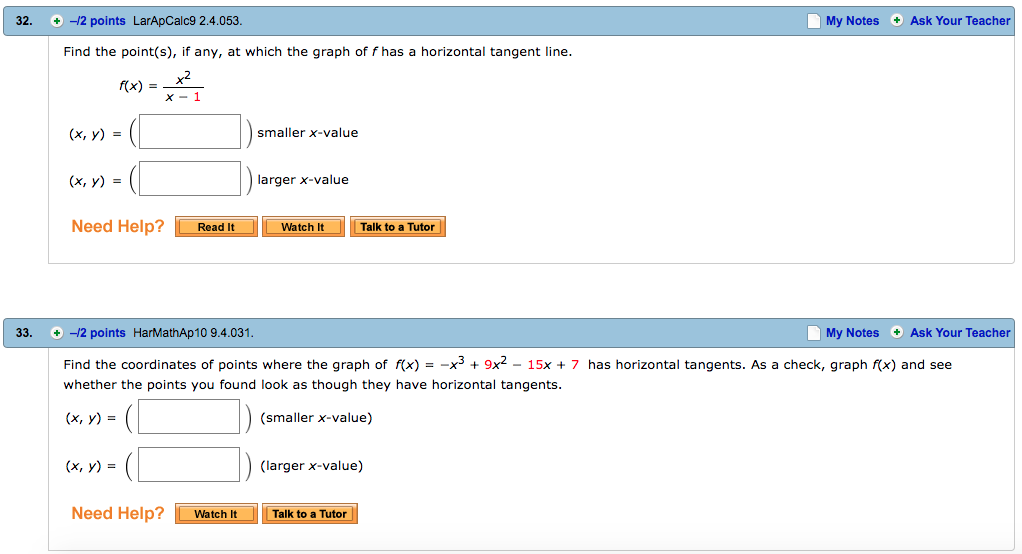
F Where The Tangent Line Is Horizontal To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function. In the area of calculus, a normal line is the line that touches a curve at one point and is perpendicular with the tangent line at the same point. The slope of the normal line will be the opposite reciprocal of the derivative of the tangent line.
Most mathematicians and historians agree that calculus was developed independently by the Englishman Isaac Newton (1643–1727) and the German Gottfried Leibniz (1646–1716), whose images appear in Figure. Both mathematicians benefited from the work of predecessors, such as Barrow, Fermat, and Cavalieri. The initial relationship between the two mathematicians appears to have been amicable; however, in later years a bitter controversy erupted over whose work took precedence. Although it seems likely that Newton did, indeed, arrive at the ideas behind calculus first, we are indebted to Leibniz for the notation that we commonly use today.
A vertical line has undefined slope because all points on the line have the same x-coordinate. As a result the formula used for slope has a denominator of 0, which makes the slope undefined.. The derivative has many applications in "real life"; one of the most useful is to find the rate of change of one variable with respect to another.
Think of a rate of change, or sometimes called an instantaneous rate of change as how fast something is changing at a certain point, like a point in time. The study of curves can be performed directly in polar coordinates without transition to the Cartesian system. In the particular case of a circle, there's a simple way to find the derivative. Since the tangent to a circle at a point is perpendicular to the radius drawn to the point of contact, its slope is the negative reciprocal of the slope of the radius. Hence, the tangent line has slope \(-7/24\text\) In general, a radius to the point \(\ds (x,\sqrt)\) has slope \(\ds \sqrt/x\text\) so the slope of the tangent line is \(\ds \text\) as before.
It is NOT always true that a tangent line is perpendicular to a line from the origin—don't use this shortcut in any other circumstance. Now write the equation in point-slope form then algebraically manipulate it to match one of the slope-intercept forms of the answer choices. What's basically happening with this equation is each iteration takes you closer and closer to the true solution, as the following image shows. The blue line is the tangent line for x0 and the green line is the tangent line for the second iteration. Eventually, your answers will get closer and closer to the red x-value. Vertical cusps are where the one sided limits of the derivative at a point are infinities of opposite signs.
Vertical tangent lines are where the one sided limits of the derivative at a point are infinities of the same sign. The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator. Because if we are ever asked to solve problems involving the slope of a tangent line, all we need are the same skills we learned back in algebra for writing equations of lines. The limit definition of the slope of the tangent line at a point on the graph of a function. For a general curve, finding the tangent line is also done by finding the solutions to two equations in two unknowns found in a similar manner as above. However, it might require the use of 'fzero' or even 'fsolve' to find the solutions, depending on the nature of the curve's equation.
These two equations lead to a simple quadratic equation in x which has either two solutions, one solution, or none, depending on , and therefore a similar number of possible tangent lines. Continuity of First Partials Implies Differentiability further explores the connection between continuity and differentiability at a point. This theorem says that if the function and its partial derivatives are continuous at a point, the function is differentiable. When working with a function of two variables, the tangent line is replaced by a tangent plane, but the approximation idea is much the same. Calculating the equation of a tangent plane to a given surface at a given point.
We learned about the equation of a plane in Equations of Lines and Planes in Space; in this section, we see how it can be applied to the problem at hand. Use the tangent plane to approximate a function of two variables at a point. The instantaneous rate of change of a function \(f\) at a value \(a\) is its derivative \(f′\). We obtained the same value for the slope of the tangent line by using the other definition, demonstrating that the formulas can be interchanged. As \(h\to 0\), these secant lines approach the tangent line, a line that goes through the point \((2,f)\) with the special slope of \(-64\).
In parts and of Figure 2.2, we zoom in around the point \(\). In we see the secant line, which approximates \(f\) well, but not as well the tangent line shown in . What we are really computing is the average velocity on the interval \([2,2+h]\) for small values of \(h\). That is, we are computing \[\frac\]where \(h\) is small. You don't know the tangent's equation yet, but you can already tell that its slope is negative, and that its y-intercept is negative (well below the parabola vertex with y value -5.5).